Correlation

MATH 4720/MSSC 5720 Introduction to Statistics

Dr. Cheng-Han Yu
Department of Mathematical and Statistical Sciences
Marquette University

Correlation

Relationship Between 2 Numerical Variables

• Depending on the situation, one of the variables is the explanatory variable and the other is the response variable. (Discussed in Regression)

• There is not always an explanatory-response relationship.

• Examples:

  • height and weight

  • income and age

  • SAT/ACT math score and verbal score

  • amount of time spent studying for an exam and exam grade

Can you provide an example that 2 variables are associated?

Scatterplots

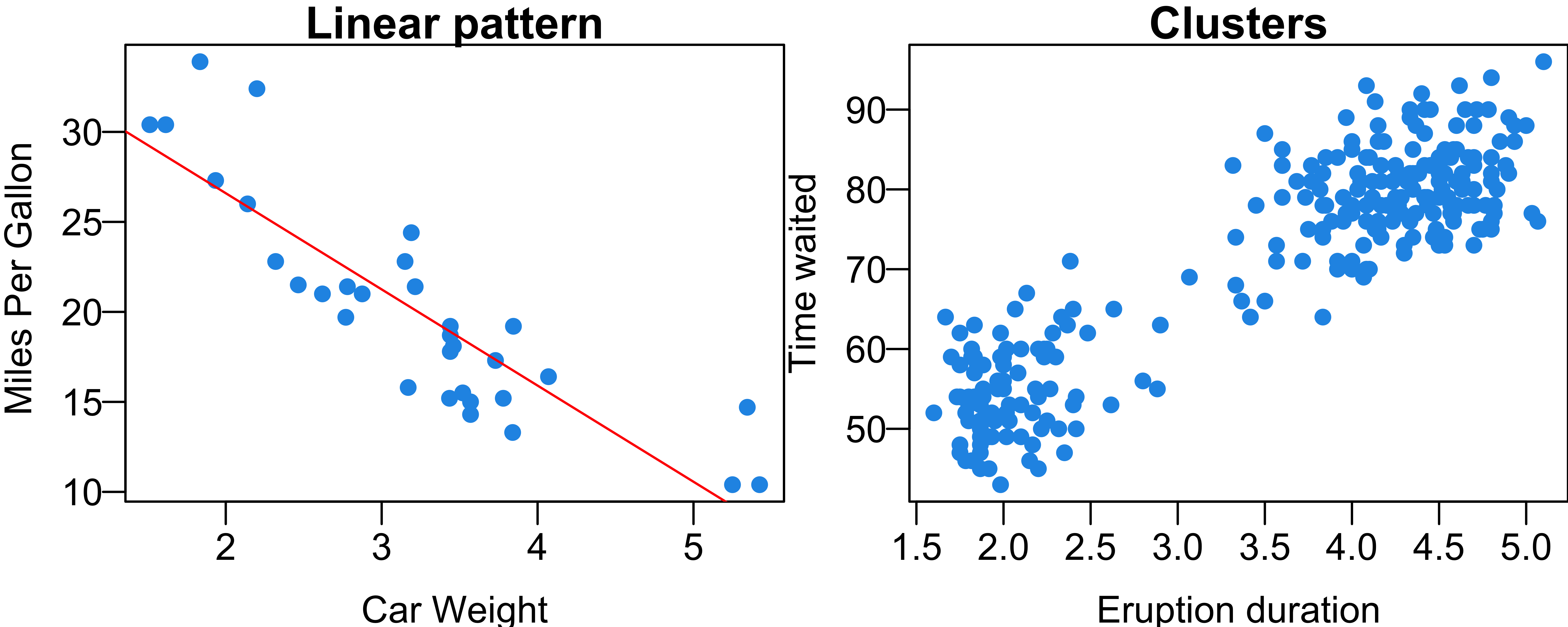
• Describe the overall pattern
  • Form: linear or clusters
  • Direction: positively associated or negatively associated
  • Strength: how close the points lie to a line/curve

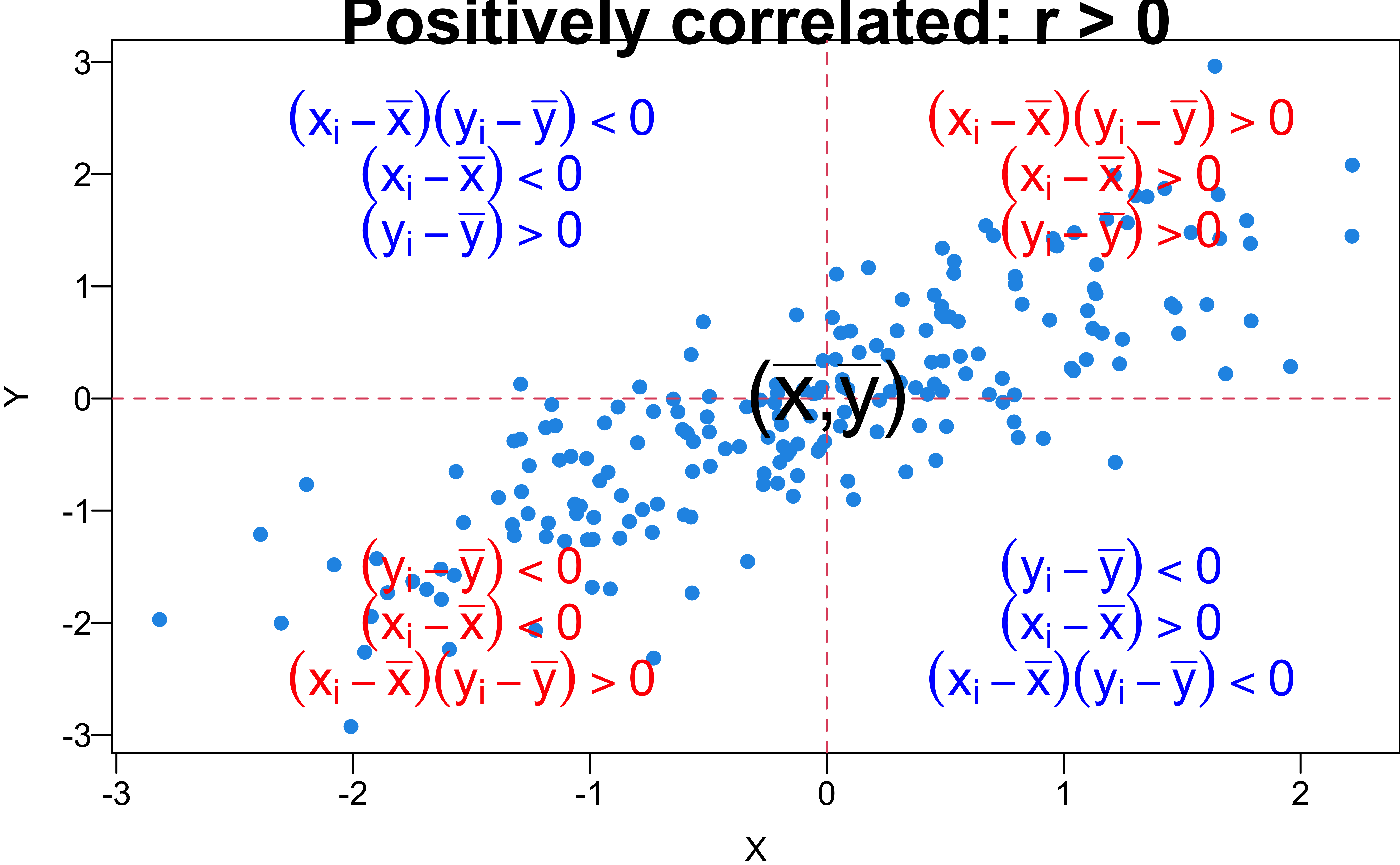
Linear Correlation Coefficient

• The sample correlation coefficient, denoted by \(r\), measures the direction and strength of the linear relationship between two numerical variables: \[\small r :=\frac{1}{n-1}\sum_{i=1}^n\left(\frac{x_i-\overline{x}}{s_x}\right)\left(\frac{y_i-\overline{y}}{s_y}\right) = \frac{1}{(n-1) (s_xs_y)}\sum_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)\]

• \(-1 \le r\le 1\)
• \(r > 0\): The larger value of \(X\) is, the larger value of \(Y\) tends toward.
• \(r = 1\): Perfect positive linear relationship.

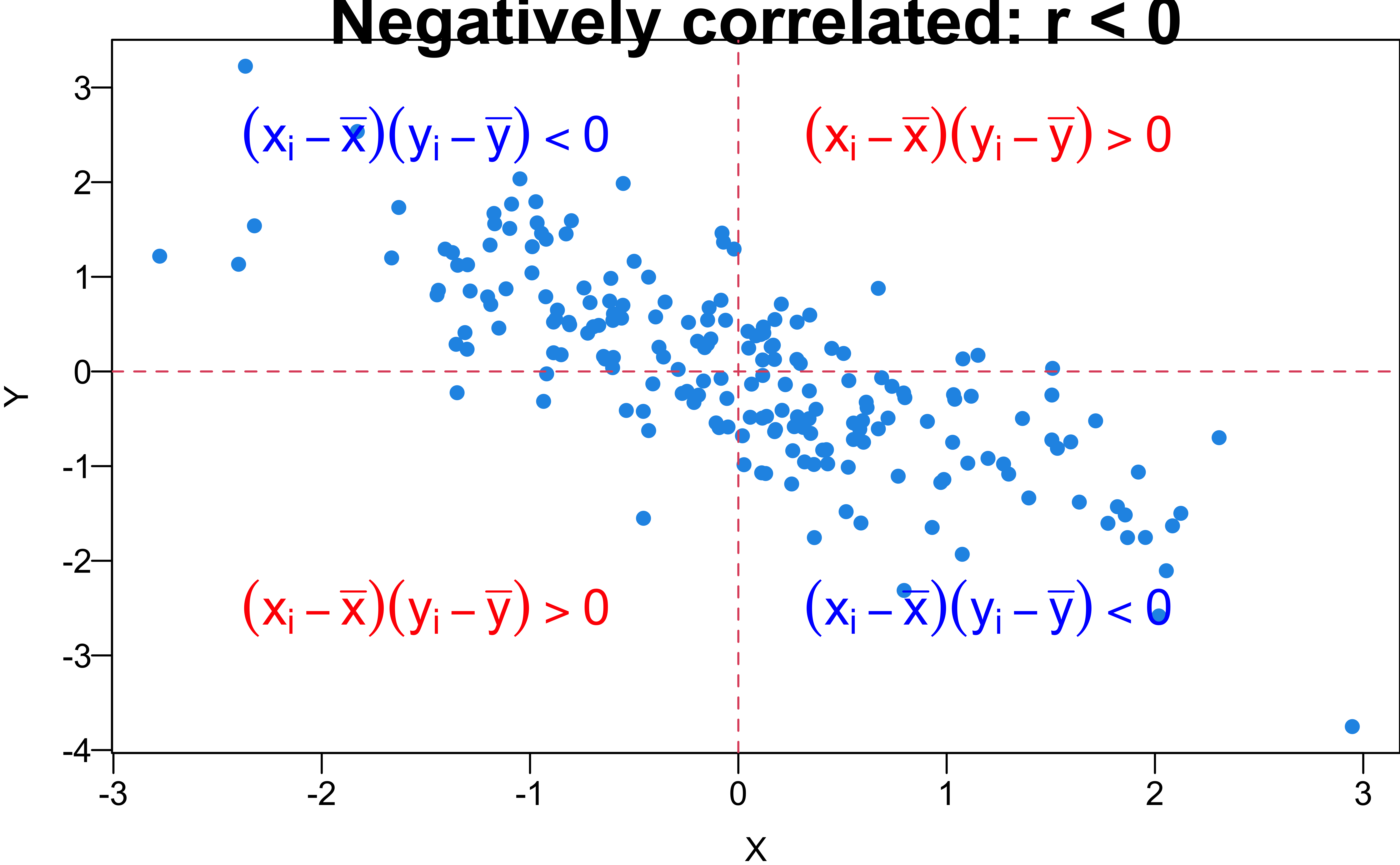
Linear Correlation Coefficient

• The sample correlation coefficient, denoted by \(r\), measures the direction and strength of the linear relationship between two numerical variables: \[\small r :=\frac{1}{n-1}\sum_{i=1}^n\left(\frac{x_i-\overline{x}}{s_x}\right)\left(\frac{y_i-\overline{y}}{s_y}\right)\]

• \(-1 \le r\le 1\)
• \(r < 0\): The larger value of \(X\) is, the smaller value of \(Y\) tends toward.
• \(r = -1\): Perfect negative linear relationship.

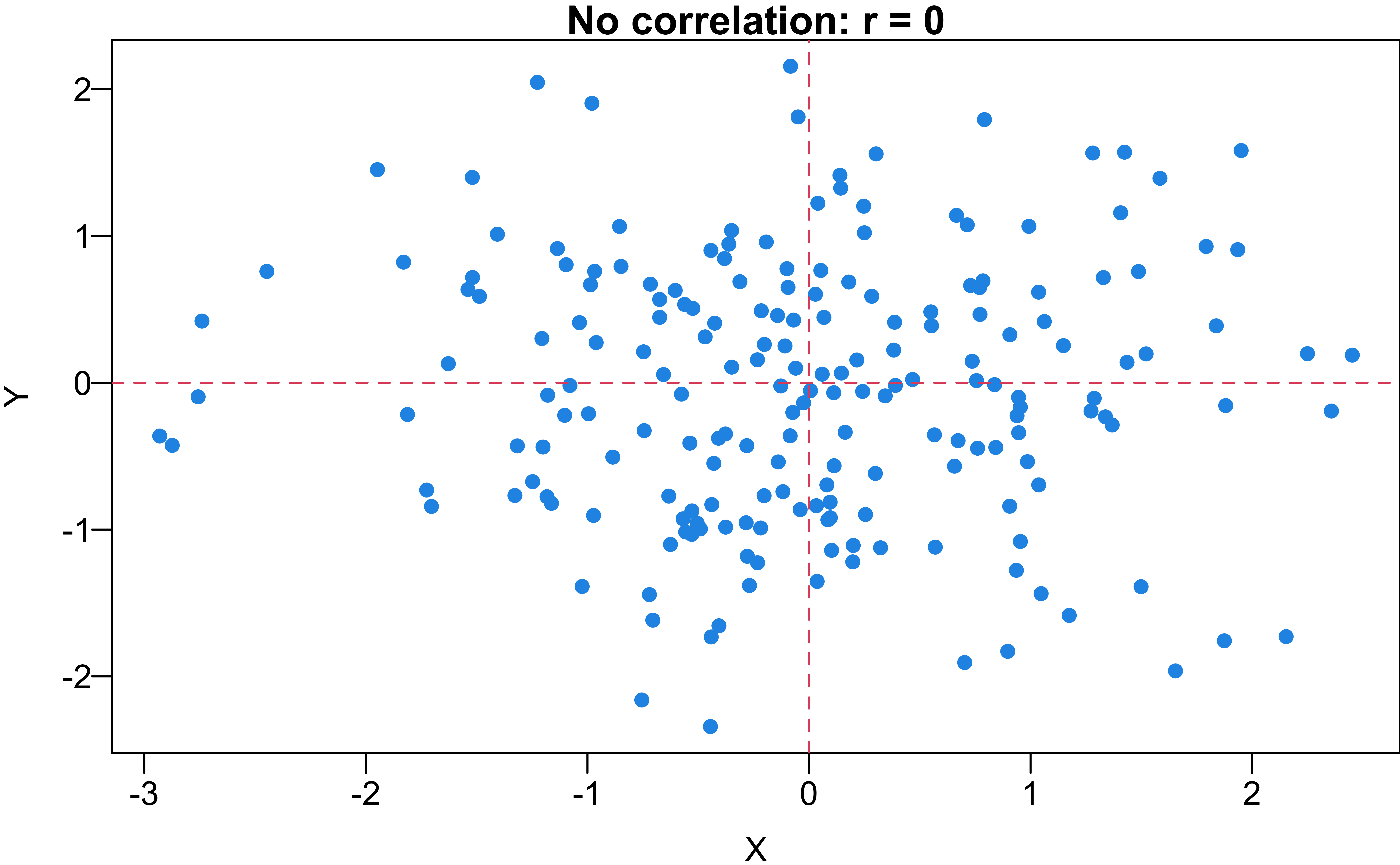
Linear Correlation Coefficient

• The sample correlation coefficient, denoted by \(r\), measures the direction and strength of the linear relationship between two numerical variables: \[\small r :=\frac{1}{n-1}\sum_{i=1}^n\left(\frac{x_i-\overline{x}}{s_x}\right)\left(\frac{y_i-\overline{y}}{s_y}\right)\]

• \(r = 0\): No linear relationship.
• If explanatory and response are switched, \(r\) remains the same.
• \(r\) has no units of measurement, so scale changes do not affect \(r\).

• Properties
  • \(-1 \le r\le 1\).
  • If \(r\) is negative, variables \(X\) and \(Y\) are negatively related. That is, the larger value of \(X\) is, the smaller value of \(Y\) tends toward.
  • If \(r = -1\), there is a perfect negative linear relationship.
  • If \(r\) is positive, variables \(X\) and \(Y\) are positively related. That is, the larger value of \(X\) is, the larger value of \(Y\) tends toward.
  • If \(r = 1\), there is a perfect positive linear relationship.
  • If \(r = 0\), there is no linear relationship.
  • If explanatory and response are switched, \(r\) remains the same.
  • \(r\) has no units of measurement associated with it.
  • Scale changes do not affect \(r\).

Correlation Example

• It is possible that there is a strong relationship between two variables but still \(r = 0\).

https://upload.wikimedia.org/wikipedia/commons/d/d4/Correlation_examples2.svg

Example in R

plot(x = mtcars$wt, y = mtcars$mpg, 
     main = "MPG vs. Weight", 
     xlab = "Car Weight", 
     ylab = "Miles Per Gallon", 
     pch = 16, col = 4, las = 1)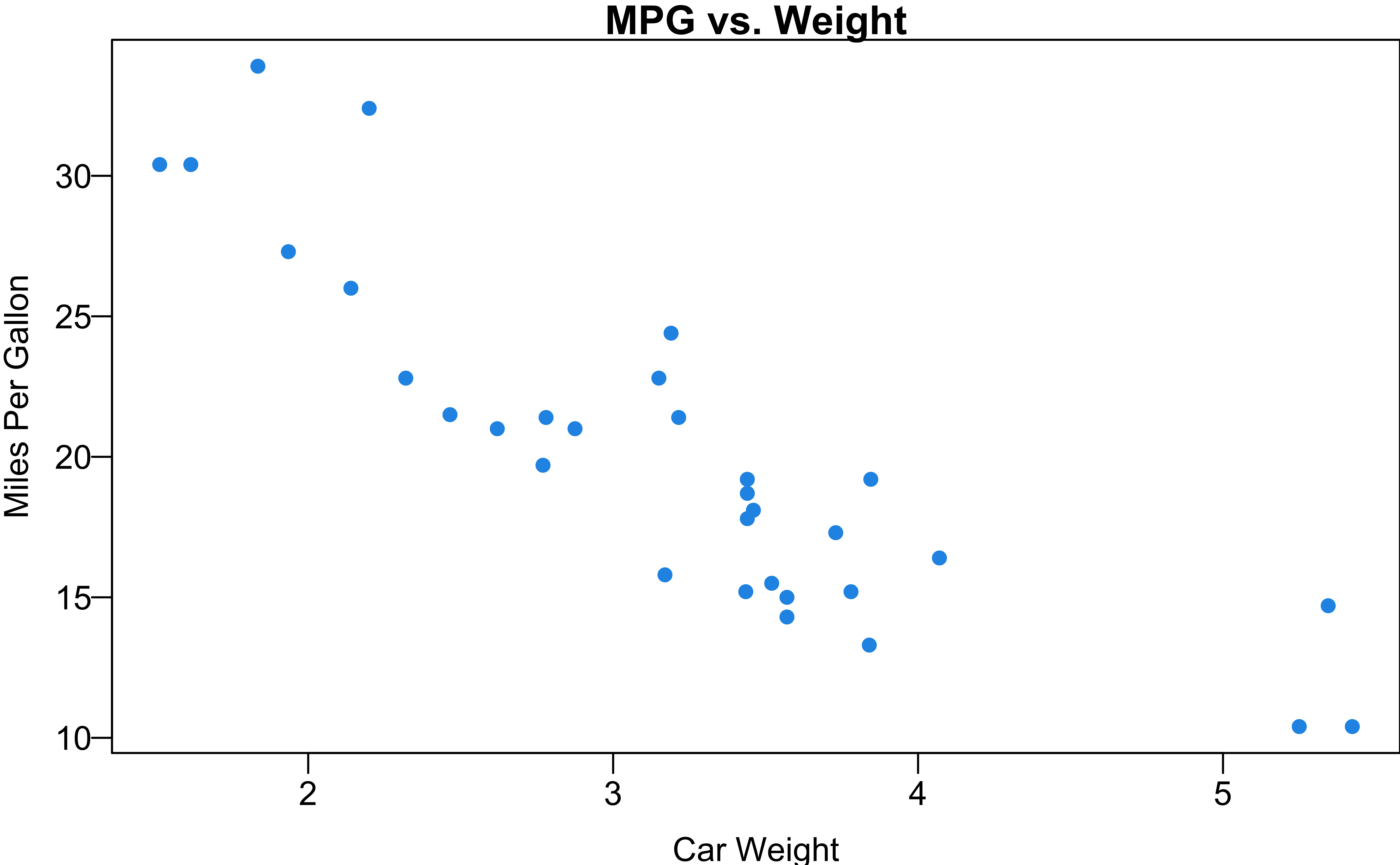

cor(x = mtcars$wt,
    y = mtcars$mpg)

[1] -0.87